剑指offer——7.裴波那契数列

1.题目

大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项。（n<=39）
斐波那契数列公式为：

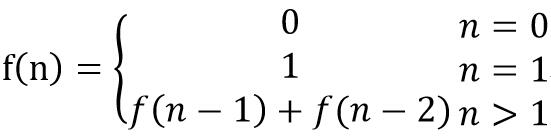
2.思路分析

我们可以以求解f（10）为例来分析递归的求解过程。想要求得f（10），我们要先知道f（9）和f（8）。同样的，要求得f（9），需要先知道f（8）和f（7）。。。我们可以使用树形结构来表示这种依赖关系，如下图所示。

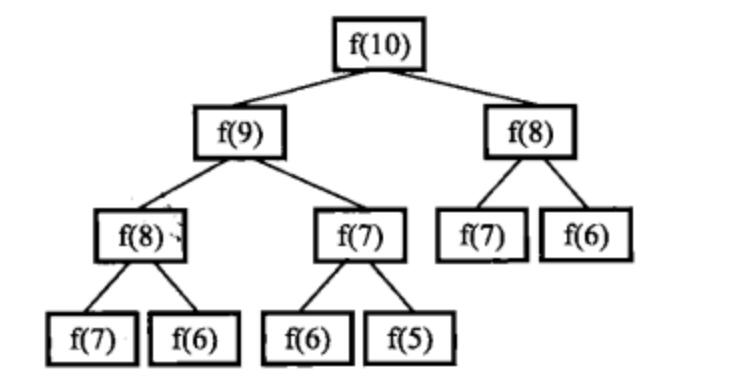
    不难发现在这棵树中有许多的节点都是重复的，而且重复的节点数会随着n的增大而急剧增加，这意味着计算量会随着n的增大而急剧增大。事实上用递归方法计算的时间复杂度是以n的指数方式递增的。改进上述方法并不难，只要想办法避免重复计算就可以了，比如可以将已经得到的数列中间项保存起来，如果下次需要计算的话先查找一下，已经计算过的就不用重复再计算了。
    更简单的办法是从下往上计算，即使用简单的循环方法来实现。

3.代码实现

C++：

class Solution {
   public:
       int Fibonacci(int n) {
           if(n <= 0){
               return 0;
           }
           if(n ==1 ){
               return 1;
           }
           int first = 0,second = 1,third = 0;
           for(int i = 2;i <= n;i++){
               third = first + second;
               first = second;
               second = third;
           }
           return third;
       }
   };

Python2.7：

class Solution:
       def Fibonacci(self, n):
           # write code here
           if n <= 1:
               return n
           first, second, third = 0, 1, 0
           for i in range(2, n+1):
               third = first + second
               first = second
               second = third
           return third